Pengertian analisis regresi

Analisis regresi adalah seperangkat metode statistik yang digunakan untuk memperkirakan hubungan antara variabel dependen dan satu atau lebih variabel independen. Ini dapat digunakan untuk menilai kekuatan hubungan antara variabel dan untuk pemodelan hubungan masa depan antara mereka.

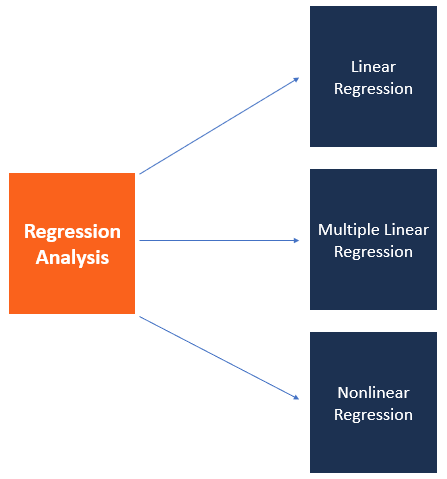
Analisis regresi

Analisis regresi meliputi beberapa variasi, seperti linier, linier berganda, dan nonlinier. Model yang paling umum adalah linier sederhana dan linier berganda. Analisis regresi nonlinier biasanya digunakan untuk kumpulan data yang lebih rumit di mana variabel dependen dan independen menunjukkan hubungan nonlinier.

Analisis regresi menawarkan banyak aplikasi dalam berbagai disiplin ilmu, termasuk keuangan.

Analisis Regresi – Asumsi Model Linier

Analisis regresi linier didasarkan pada enam asumsi mendasar:

• Variabel dependen dan independen menunjukkan hubungan linier antara kemiringan dan intersep.
• Variabel bebas tidak acak.
• Nilai residual (kesalahan) adalah nol.
• Nilai residual (kesalahan) konstan di semua pengamatan.
• Nilai residual (kesalahan) tidak berkorelasi di semua pengamatan.
• Nilai residual (kesalahan) mengikuti distribusi normal.

Analisis Regresi – Regresi Linier Sederhana

Regresi linier sederhana adalah model yang menilai hubungan antara variabel dependen dan variabel independen. Model linier sederhana dinyatakan dengan menggunakan persamaan berikut:

Y = a + bX + e

Di mana:

• Y – Variabel terikat
• X – Variabel bebas (penjelas)
• a – mencegat
• b – Kemiringan
• e – Residu (kesalahan)

Analisis Regresi – Regresi Linier Berganda

Analisis regresi linier berganda pada dasarnya mirip dengan model linier sederhana, dengan pengecualian bahwa beberapa variabel independen digunakan dalam model. Representasi matematis dari regresi linier berganda adalah:

Y = a + bX1 + cX2 + dX3 + e

Di mana:

• Y – Variabel terikat
• X1, X2, X3 – Variabel bebas (penjelas)
• a – mencegat
• b, c, d – Lereng
• e – Residu (kesalahan)

Regresi linier berganda mengikuti kondisi yang sama dengan model linier sederhana. Namun, karena ada beberapa variabel independen dalam analisis linier berganda, ada kondisi wajib lain untuk model:

Non-kolinearitas: Variabel independen harus menunjukkan korelasi minimum satu sama lain. Jika variabel independen sangat berkorelasi satu sama lain, akan sulit untuk menilai hubungan yang benar antara variabel dependen dan independen.

Analisis regresi dalam keuangan

Analisis regresi hadir dengan beberapa aplikasi di bidang keuangan. Misalnya, metode statistik merupakan dasar Capital Asset Pricing Model (CAPM). Pada dasarnya, persamaan CAPM adalah model yang menentukan hubungan antara pengembalian yang diharapkan dari suatu aset dan premi risiko pasar.

Analisis ini juga digunakan untuk meramalkan pengembalian sekuritas, berdasarkan faktor yang berbeda, atau untuk meramalkan kinerja bisnis.

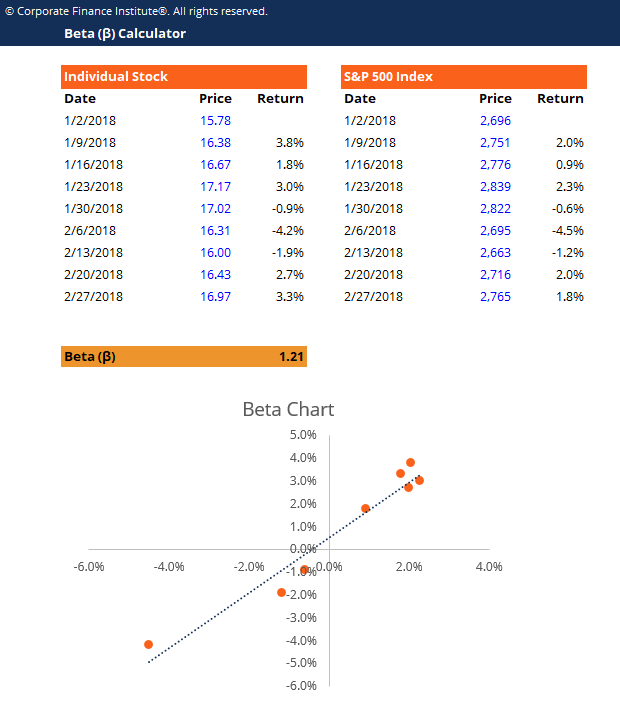
Beta dan CAPM

Di bidang keuangan, analisis regresi digunakan untuk menghitung Beta (volatilitas pengembalian relatif terhadap pasar secara keseluruhan) untuk suatu saham. Itu bisa dilakukan di Excel menggunakan fungsi Slope.

Peramalan pendapatan dan beban

Saat meramalkan laporan keuangan untuk sebuah perusahaan, mungkin berguna untuk melakukan analisis regresi berganda untuk menentukan bagaimana perubahan asumsi atau penggerak bisnis tertentu akan berdampak pada pendapatan atau pengeluaran di masa depan. Misalnya, mungkin ada korelasi yang sangat tinggi antara jumlah tenaga penjualan yang dipekerjakan oleh perusahaan, jumlah toko yang mereka operasikan, dan pendapatan yang dihasilkan bisnis.

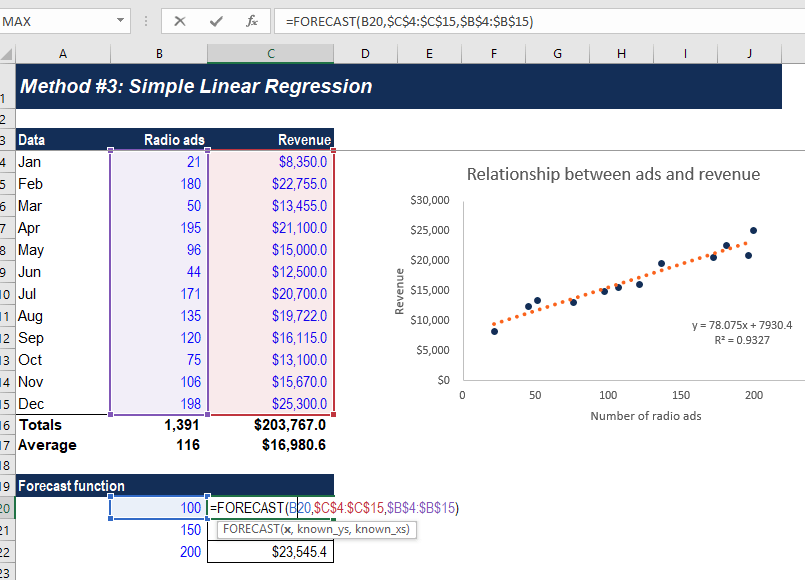
Contoh di atas menunjukkan cara menggunakan fungsi Forecast di Excel untuk menghitung pendapatan perusahaan, berdasarkan jumlah iklan yang dijalankannya.

Alat regresi

Excel tetap menjadi alat yang populer untuk melakukan analisis regresi dasar di bidang keuangan, namun, ada banyak alat statistik yang lebih canggih yang dapat digunakan.

Python dan R adalah bahasa pengkodean yang kuat yang telah menjadi populer untuk semua jenis pemodelan keuangan, termasuk regresi. Teknik-teknik ini membentuk bagian inti dari ilmu data dan pembelajaran mesin di mana model dilatih untuk mendeteksi hubungan ini dalam data.